Measuring Water Usage, OCR, and Straight Lines
2015 04 12
I decided it would be fun (i.e, just for shits and grins) to be able to read my water meter and log it using rrdtool. Easy, right? Bzzzt. Wrong!
I optimistically hooked up a Raspberry Pi and my motion activated image capture software in order to see what the meter looked like.
This is what my water meter looks like:

And this is what my water meter looks like on drugs:

Fans of image processing will recognize that these are two completely different things. Night and day.
How do I extract the meter reading?
My very first attempt was to use the excellent PNM tools to extract just the digital readout:
jpegtopnm input.jpg | pnmcut -left 335 -right 530 -top 130 -bottom 185 | pnmtojpeg >output.jpg
Which gave me an image like this:

I figured, “this is going to be easy, just find a public domain OCR package and I'm done!”
Yeah, well, that didn't work out. I tried tesseract, gocr, and a third one I can't remember right at this point. None of the readily available OCR packages could read 6 digits in a row. Not a one. They didn't even give me ONE digit. Just blank stares.
I then though, “what do I really want to measure?” I want to measure the little things. Notice that the meter is in m3. I'm in Canada, eh? and we measure water in Litres and cubic metres (m3). (And yes, the Canadian spelling for the unit of measure is “metre,” whereas a device that measures something is called a “meter.” LOL.) The red dial goes around once to indicate ten litres, which means that each of the little ticks on the meter is 100 mL. The Czech beer I drink comes in 500 mL cans, for reference, so it would take 20 beers to go once around the dial.
If I could “human OCR” the digits just once, and then tell the program to pay attention to the little red indicator, I could have the program give me very accurate readings of my water meter.
How to detect a red indicator
Of course, the real trick is to detect the red indicator, especially in the varying light conditions shown above.
I tried a number of methods, but the one that eventually stuck was to look for pixels where the overall intensity was greater than a small threshold, and where the red intensity was bigger than the green or blue intensity by at least a small threshold:
for (x = 0; x < w; x++) {
for (y = 0; y < h; y++) {
v = src (x, y); // fetch pixel
r = (v >> 16) & 0xff; // get red,
g = (v >> 8) & 0xff; // green,
b = v & 0xff; // and blue, and
v = ((r + g + b) / 3) & 0xff; // convert it to black & white
// calculate target pixel
dst (x, y, v > 10 && (r - g > 5 || r - b > 5) ? 0xff0000 : 0);
}
}
With the light and dark images, I got:


So far so good!
Searching on the web for “how to find straight lines in image” or “line detection algorithm” etc. resulted in hits that weren't useful.
So I opted for one more piece of “Human OCR” — the location of the indicator's axis. Turns out it's at (445, 232) on the image. Armed with this last fact, I again searched for how to find a single straight line, and again didn't find anything terribly useful.
Think, man!
How about if we looked at concentric circles around the indicator's axis, and found pixels that were all in a straight line?

The algorithm generates concentric circles, centered at the indicator's axis. For each pixel on the circle, see if it hits a red pixel or not. If it hits a red pixel, then add a weighted value to the count being kept for that specific angle. Perhaps the code will be clearer:
// calculate circles
double angles [360];
for (a = 0; a < 360; a++) {
angles [a] = 0;
for (radius = 150; radius > 0; radius -= 5) {
x = (double) radius * cos ((double) a / 360. * 2. * PI) + 445;
y = (double) radius * sin ((double) a / 360. * 2. * PI) + 232;
if (srct (x, y)) {
angles [a] += radius;
}
// draw concentric circles
dst (x, y, 0xffff00);
}
}
This code goes through all 360 degrees (one degree at a time) and generates the circle points at each radius (150 to 5, by steps of 5).
If the pixel at that point is illuminated, then the radius value is added to the angle count.
I used the value of the radius instead of 1 because I wanted to give more weight to the tip of the indicator rather than the axis.
That's because there's this weird distortion (some kind of magnifying glass type of thing) at the left side of the readout value:

Horribly inefficient code, I know — I could:
- keep the sin/cos values in a table,
- look at only a few degrees difference from the previous indicator's position,
- do 100 angles, not 360 (because the output is only 1 in 100 accurate), and so on.
But, “keep it simple,” and “early optimization is the root of all evil” are what I go by.
Finally, it's a simple matter to find the best match for the angle, and convert that to a litres and 100's of millilitres value:
// find angle with the most hits
y = 0;
for (x = 0; x < 360; x++) {
if (angles [x] > angles [y]) {
y = x;
}
}
// convert y to actual angle on image
y = (y + 90) % 360;
if (state == Primed && y < 5) {
optB += 10;
state = Crossing;
} else if (state == Crossing && y > 180) {
state = Primed;
}
// kludge
if (y >= 358) y = 358;
printf ("%s %.1f L\n", f, optB + (double) y / 36.);
This looks to see if the angle at x has more hits than the angle at y, and updates y if so. y ends up indicating the angle with the most hits.
The dial has the 0.0 position at the top of the image, whereas 0 degrees is actually at the rightmost part of the dial. So we add 90 to y to convert it (and keep it in range 0..359 via the modulo operator).
Next, I keep a state variable (called, oddly enough, state), which is either Primed or Crossing. The idea is that I can't be 100% sure (given lighting condition variations etc.) that the dial might not go backwards by an infinitesimal amount, screwing up my calculation.
To that end, optB is the “Human OCR” starting value of the meter, and I increment it by 10 litres every time the indicator crosses the 0.0 mark.
Finally, there's a tiny kludge to prevent %.1f from rounding up to 10.0 (from 9.9) on me, and then finally the printout.
Summary
The input to this program is a series of JPEG images; the output is a series of filename and litre values.
With a teensy post-processing program and a script, I can feed this into rrdtool.
The output is like this:
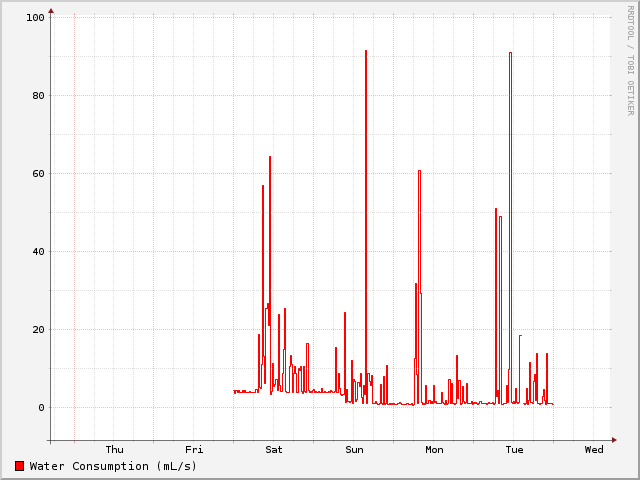
Yes, the output really is in millilitres per second. You can see where the whole "raison d'etre" for the project began. Look at the baseline water consumption up to the “S” in “Sunday” — there's a leakage of 5mL/s or so (18L/hour) corresponding to the broken faucet in the back yard. It started leaking around December, as near as I can tell. We initially attributed the “wow that's expensive!” water bills we were getting to a new shower head that we had installed. It never occurred to us to check the back yard (the faucet is under the deck, and there was lots of snow there; no reason to go and look).
LOL. But now, I can see “at a glance” what's going on.
2015 04 24
You can also see another baseline artefact.
Once the leak was fixed on Sunday, notice how the consumption never really ever hits zero.
That's because we had another leak — the toilet “flap” was old, and was leaking water from the tank
into the bowl, causing the toilet to occasionally get a burst of water to keep the tank full.
A $10 visit to Home Depot and voila, the problem is fixed:
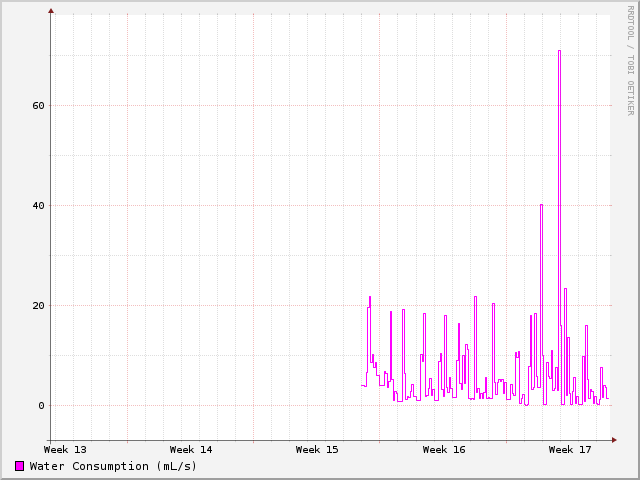
In the above picture, you can see that the baseline actually touches the zero mark periodically.